首先简要介绍一下欺骗神经网络的原理:
输入数据微小的改变,可能大幅度地影响输出。
神经网络中几乎到处都有这种机会。例如 sigmoid 函数,自变量在 0 附近的微小改变可以引发函数值很大的变化。一个全连接层,各个节点都变动一个微小数值,没准就能齐心协力把输出的 argmax 改变掉,让分类器作出错误的判断。
CTF 中也经常出现这类「指鹿为马」形式的问题:给出一个分类器(我遇到过神经网络和 k-nearest)的所有参数,然后给出一个样本 $x$,它被模型正确地识别为 $y$. 选手的任务是小幅度地修改 $x$,使得模型将之分类成 $y ^ \prime$. 这里可能要求 $x ^ \prime$ 与 $x$ 的距离小于某个值,例如求出 $x$ 与 $ x ^ \prime$ 的每个像素点之间的距离(RGB8,各个通道之差取绝对值求和),要求像素距离总和小于 $10 ^ 5$.
我们之所以可以欺骗神经网络,是因为神经网络缺乏泛化能力。一般来看,过拟合越严重,我们越能轻易地(指 $x ^ \prime$ 与 $x$ 距离很近)修改输入向量,来让神经网络输出我们想要的值。
这是如何做到的?回顾神经网络的训练过程:
- 在网络中计算 output
- 求出 output 与 label 的误差,并求出各个网络参数的梯度
- 利用刚刚求出的梯度,更新网络参数
而我们要欺骗一个已有的神经网络,可以这样做:
- 在网络中计算 output
- 求出 output 与我们想要篡改到的 target 的误差,求出图片的梯度
- 冻结网络的参数,而去对图片进行梯度下降
重复上述过程若干次,可以让神经网络产生误判。
作为演示,我们接下来实现一个神经网络,它识别 MNIST 数据集的手写数字。然后我们随便找一张图像,将其修改一番,使得我们人类仍然能够正确识别,而神经网络给出错误判断。
实现神经网络
作为 PyTorch 玩家,我们当然用 PyTorch 来完成此项工作。先把包导入进来:
import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt 然后导入数据集。 torchvision 库可以帮助我们快速导入 MNIST.
trans_to_tensor = transforms.Compose([
transforms.ToTensor()
])
data_train = torchvision.datasets.MNIST(
'./data',
train=True,
transform=trans_to_tensor,
download=True)
data_test = torchvision.datasets.MNIST(
'./data',
train=False,
transform=trans_to_tensor,
download=True)
data_train, data_test
'''
(Dataset MNIST
Number of datapoints: 60000
Root location: ./data
Split: Train
StandardTransform
Transform: Compose(
ToTensor()
),
Dataset MNIST
Number of datapoints: 10000
Root location: ./data
Split: Test
StandardTransform
Transform: Compose(
ToTensor()
))
'''ToTensor() 将其变换为 Tensor接下来,弄一个训练数据的 loader:
train_loader = torch.utils.data.DataLoader(
data_train,
batch_size=100,
shuffle=True)
next(iter(train_loader))
'''
[tensor([[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
...,
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]]]),
tensor([0, 1, 4, 4, 6, 7, 7, 8, 3, 2, 6, 6, 5, 2, 9, 6, 3, 6, 4, 7, 1, 8, 5, 9,
8, 0, 2, 5, 3, 3, 4, 3, 2, 4, 8, 3, 4, 1, 7, 2, 7, 5, 4, 3, 8, 3, 0, 9,
1, 5, 8, 7, 6, 9, 5, 4, 9, 8, 6, 1, 0, 3, 3, 0, 0, 4, 5, 1, 8, 6, 0, 3,
2, 0, 0, 2, 7, 1, 2, 8, 6, 9, 3, 6, 1, 0, 1, 6, 1, 3, 8, 2, 3, 8, 0, 4,
0, 1, 0, 0])]
'''来展示一个数据看看:
x, y = next(iter(train_loader))
plt.imshow(x[0].squeeze(0), cmap='gray'), y[0]
现在来定义我们的网络。它接收 $28 \times 28$ 的图像,将其摊平成 $784$ 个特征维度的向量。经过一个全连接层,生成 $100$ 维度的特征,激活函数为 ReLU;再经过一个全连接层,生成 $10$ 维度的预测向量,激活函数为 Sigmoid.
class MyNet(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(28*28, 100)
self.fc2 = nn.Linear(100, 10)
def forward(self, x):
x = x.view(-1, 28*28)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = torch.sigmoid(x)
return xview() 展开接下来生成一个神经网络实例:
net = MyNet()
device = torch.device('cuda:0')
net.to(device)
net
'''
MyNet(
(fc1): Linear(in_features=784, out_features=100, bias=True)
(fc2): Linear(in_features=100, out_features=10, bias=True)
)
'''定义损失函数和优化器:
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters())现在来训练网络。
def fit(net, epoch=1):
net.train()
run_loss = 0
for num_epoch in range(epoch):
print(f'epoch {num_epoch}')
for i, data in enumerate(train_loader):
x, y = data[0].to(device), data[1].to(device)
outputs = net(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
run_loss += loss.item()
if i % 100 == 99:
print(f'[{i+1} / 600] loss={run_loss / 100}')
run_loss = 0
test(net)
def test(net):
net.eval()
test_loader = torch.utils.data.DataLoader(data_train, batch_size=10000, shuffle=False)
test_data = next(iter(test_loader))
with torch.no_grad():
x, y = test_data[0].to(device), test_data[1].to(device)
outputs = net(x)
pred = torch.max(outputs, 1)[1]
print(f'test acc: {sum(pred == y) / outputs.shape[0]}')
net.train()开始训练:
fit(net, epoch=5)
'''
epoch 0
[100 / 600] loss=1.512832807302475
test acc: 0.9493999481201172
[200 / 600] loss=1.5147511053085327
test acc: 0.9512999653816223
[300 / 600] loss=1.5131039583683015
test acc: 0.9527999758720398
[400 / 600] loss=1.5105569410324096
test acc: 0.9528999924659729
[500 / 600] loss=1.5110788369178771
test acc: 0.9526000022888184
[600 / 600] loss=1.5110698103904725
test acc: 0.9556999802589417
...
epoch 4
[100 / 600] loss=1.49038764834404
test acc: 0.9696999788284302
[200 / 600] loss=1.4929101729393006
test acc: 0.9692999720573425
[300 / 600] loss=1.490309545993805
test acc: 0.9702999591827393
[400 / 600] loss=1.4926683104038239
test acc: 0.9710999727249146
[500 / 600] loss=1.4924321293830871
test acc: 0.9702000021934509
[600 / 600] loss=1.488825489282608
test acc: 0.9722999930381775
'''我们这个双层感知机取得了 97.23% 的准确率。接下来我们攻击之。
欺骗神经网络
首先取个图出来:
origin_img, origin_tag = next(iter(train_loader))
origin_img = origin_img[0]
origin_tag = origin_tag[0]
plt.imshow(origin_img.view(28, 28), cmap='gray'), origin_tag
现在我们想欺骗神经网络,让网络把 9 误认为 7. 我们冻结网络参数,让神经网络进行反向传播,最后对图片进行梯度下降:
def play(epoch):
for num_epoch in range(epoch):
net.requires_grad_(False)
img.requires_grad_(True)
loss_fn = nn.CrossEntropyLoss()
output = net(img)
target = torch.tensor([7]).to(device)
loss = loss_fn(output, target)
loss.backward()
img.data.sub_(img.grad * .05)
img.grad.zero_()
net.requires_grad_(True)
if num_epoch % 100 == 99:
print(f'[{num_epoch + 1} / {epoch}] loss: {loss} pred: {torch.max(output, 1)[1].item()}')
if torch.max(output, 1)[1].item() == 7:
print(f'done in round {num_epoch + 1}')
return
img = origin_img.detach().to(device).view(1, 28, 28)
img.requires_grad_(True)
play(1000)
'''
[100 / 1000] loss: 2.4601898193359375 pred: 9
[200 / 1000] loss: 1.6000720262527466 pred: 9
done in round 207
'''我们发现,在迭代 207 次之后,神经网络就把图片误认为是 7 了。来看一下原图和新图的对比:
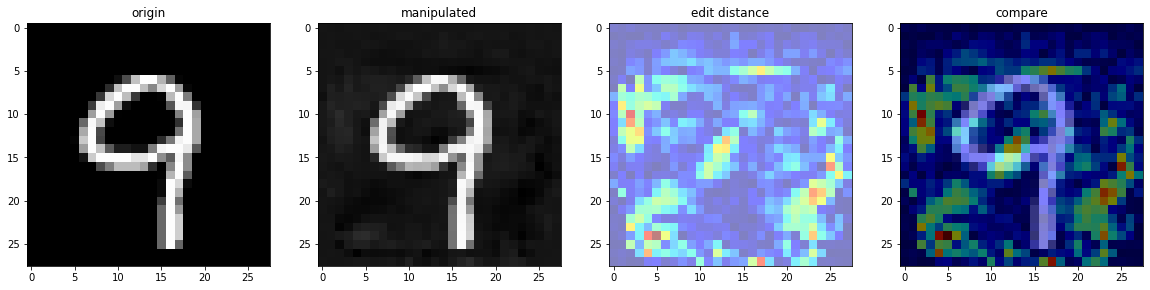
人眼能轻易地识别为 9,但我们的网络判断这图是 7,于是我们成功地欺骗了神经网络。最后,来欣赏一张关于神经网络泛化能力的漫画:

