RSA是一种非对称加密算法。谓之“非对称”,是因为加密和解密使用的是不同的密钥。RSA算法利用公钥来加密,用私钥来解密;公钥可以随意公布,任何人都可以利用公钥来加密一条信息,但只有私钥持有者才能把信息解密。
这是非常有用的加密体系。譬如,Alice 想给 Bob 发送一条信息,那么她可以在网上找到 Bob 的公钥,然后加密信息,并通过随便什么渠道传送给 Bob. 假设有一位窃听者 Eve 得到了加密后的信息,他也无法解密,因为没有私钥。
RSA另有一个特点:用私钥加密的信息,用公钥可以解密。这让基于RSA的数字签名成为可能。假如我写了一篇文章,我可以用私钥加密这一篇文本的md5值,把密文(也就是签名)附在文章后面。读者从可信的渠道得到我的公钥,利用公钥解密签名,发现与这篇文章的md5值一致,于是可以确信这篇文章确实是我写的。
RSA是极其巧妙的算法,而它的数学基础却出奇地简单,代码实现也不复杂。RSA同时是一个难以破解的密码体系,破解RSA的速度取决于大整数分解的速度。从RSA中,我们可以看到数论在现实生活中的运用,以及令人惊叹的人类智慧。
RSA算法的发明者是:Ron Rivest、Adi Shamir、Leonard Adleman,算法提出于1977年。
RSA的数学基础
学过数论的同学,对欧拉函数不会陌生。它是一个数论函数(定义域为正整数集,值域为复数集),定义是:$\varphi(n)$ 为 $\{1, 2,3,\cdots ,n\}$ 中与$n$互质的数的个数。
举几个例子:$\varphi(6)=2$,因为6以内与6互质的数只有1和5. 而$\varphi(10)=4$,因为10以内与10互质的数有1、3、7、9,共4个。另外,不难发现,对于质数$p$,有$\varphi(p) = p-1$.
为了更深入地讨论欧拉函数的性质,我们需要知道欧拉函数的通项公式。如果您只是想知道 RSA 算法怎么写、怎么用,则下面一段可以跳过。
欧拉函数的通项公式是什么?我们先给出结论,再谈谈是如何找到这个结论的。$$\varphi(n) = n \cdot \prod_{p}(1 - \frac1p)~~,其中p是n的质因子$$
想求出$\varphi(n)$,那就得统计出 $n$ 以内有多少个与 $n$ 互质的数。那么,与 $n$ 互质的数 $r$ 有什么特点呢?关键在于: $n$ 拥有的质因子, $r$ 全都没有。换句话讲:假设 $n$ 的质因数分解为$$n = p_1^{k_1}\cdot p_2 ^ {k_2} \cdots p_c ^{k_c}$$则 $r$ 必然满足 $r \% p_1 \neq 0, r\% p_2\neq 0,\cdots$ 既然如此,研究 $r$ 模掉 $n$ 的质因子们所得到的结果,就可以看出 $r$ 的一些性质。我们来造一个函数:$G(x) = (x\% p_1^ {k_1}, ~ x\% p_2 ^ {k_2}, ~ \cdots x \% p_c ^ {k_c})$,有性质如下:
$r$ 与 $n$ 互质,当且仅当 $G(r)$ 生成的元组中,对于第 $i$ 位,总有它不能被 $p_i$ 整除。我们把这种元组称为合法元组。
这是一条很平凡的性质,但它可以成为计数的一把钥匙。直接统计 $n$ 以内与 $n$ 互质的数是困难的,但统计有多少个合法元组则简单得多。合法元组的第 $i$ 位不能是 $p_i$ 的倍数或0,那么这一位有 $p_i^{k_i} \cdot (1-\frac1{p_i})$ 种取值,故依据乘法原理,合法元组的总数是:$$\prod_{i<c}p_i ^ {k_i} (1-\frac1{p_i}) ~ = ~ \prod_{i<c}p_i ^ {k_i} \prod_{i<c}(1-\frac1{p_i}) ~ = ~ n \prod_{i<c}(1-\frac1{p_i})$$
这个式子要成为欧拉函数的通项公式,还有最后一步路要走:$G$目前只是一个普通映射,既有可能多个 $r$ 对应同一个合法元组,也可能一个合法元组对应不了任何 $r$. 从而合法元组的数量未必恰好就是与 $n$ 互质的数的数量。接下来的任务是:证明 $G: \{1,2,3,\cdots ,n\} \to (元组)$ 是一个双射。
还记得中国剩余定理(CRT)吗?它通过一个精妙的构造,指出了 $(元组)\to \{1,2,3,\cdots ,n\}$是一个双射(当然了,这个结论只是CRT的一个副产品)。中国剩余定理在这里不再赘述,感兴趣的读者可以去查阅相关资料。总之,既然元组与 $n$ 以内的整数是一一对应的,那么合法元组的数量就是 $n$ 以内与 $n$ 互质的数的个数。从而我们得到了欧拉函数的通项公式:$$\varphi(n) = n \cdot \prod_{p}(1 - \frac1p)~~,其中p是n的质因子$$
现在我们手上有欧拉函数的通项公式了。可以随便挑几个数验证一下:$$\varphi(10) = 10 \times \frac12 \times \frac45 = 4,\quad \varphi(24) = 24 \times \frac12 \times \frac23 = 8$$
利用欧拉函数的通项公式,可以得到两条性质:
- $\varphi$ 是积性函数。若 $a,b$ 互质,则有$\varphi(ab) = \varphi(a)\cdot \varphi(b)$
- 欧拉定理。若 $a, m$ 互质,则有 $a^{\varphi(m)} \equiv 1 \pmod m$
不难发现,费马小定理是欧拉定理在 $m$ 为质数下的情形。
以上这堆性质的证明、欧拉函数通项的求法、线性筛欧拉函数、扩展欧几里得算法,是接下来代码实现的基础。我一年前给高中生讲数论的时候做了篇课件,恰好涵盖了这些内容,点这里下载。
欧拉定理是欧拉函数最大的作用。利用欧拉定理可以得到结论:若$a,m$互质,则$$a^b \equiv a ^ {b \% \varphi(m)} \pmod m$$ 这不仅大大降低了计算复杂度(可以利用快速幂算法),也是 RSA 算法的基石。
RSA算法
RSA算法的过程如下:
- 随便选择两个极大的质数,分别记为 $p, q$. 当然这里 $p\neq q$.
- 记 $N = p\cdot q$, 则由欧拉函数的积性有 $\varphi(N) = (p-1)(q-1)$.
- 选取一个小于 $ N $ 的 $e$, 使得 $\gcd(e, \varphi(N))=1$. 求出 $e$ 在模 $\varphi(N)$ 意义下的逆元,记为$d$.
- 我们得到了$(N, e)$作为公钥,$(N, d)$作为私钥。
P.S. 注意到 $e$ 和 $d$ 是对称的,把 $e$ 拿去当私钥,把 $d$ 拿去当公钥也可行。
公钥可以分发给所有人,私钥必须保存好。接下来,别人可以用公钥加密信息发给我,我用私钥可以解密这条信息。下面来讨论加密、解密算法。
假设 Alice 想给 Bob 发一条信息,于是搞到了 Bob 的公钥$(N, e)$. 设 $m$ 为明文,则我们这样计算出密文:$$c \equiv m^e \pmod N$$ Bob 收到密文 $c$ 之后,用自己手上的私钥解密:$$m \equiv c^ d \pmod N$$
为什么这样就可以恢复出明文 $m$?注意到$$c^d \equiv (m^e) ^ d \equiv m^{ed} \equiv m^ {ed \% \varphi(N)} \pmod N$$而 $e,d$ 在模$\varphi(N)$意义下互为逆元,故$ed \% \varphi(N) = 1$. 从而 $m^ {ed \% \varphi(N)} \equiv m \pmod N$. 证毕。
代码实现RSA加密、解密异常简单,只需要会扩展欧几里得算法、快速幂就行了。如下:
def exgcd(a, b): # 扩展欧几里得算法
if b==0: return (1, 0)
x, y = exgcd(b, a%b)
return (y, x-a//b*y)
def getInv(a, mod): # exgcd求逆元
x, y = exgcd(a, mod)
return x
# Python下负数模正数得到正数。如果是其他语言,得返回 (x % mod + mod) % mod
def quickPow(x, p, mod): # 模 mod 意义下求 x 的 p 次方
if p==0: return 1
if p==1: return x
t = quickPow(x, p//2, mod)
if p%2 == 0: return t * t % mod
return t * t * x % mod
def encrypt(m, N, e): # 加密
return quickPow(m, e, N)
def decrypt(c, N, d): # 解密
return quickPow(c, d, N)
# 拿 bsdgames 里面的 `primes` 程序随便造的 p, q
p = 100088459
q = 1000049473
N = p * q
phi = (p-1) * (q-1)
e = 2333333
d = getInv(e, phi)
c = encrypt(123454321, N, e)
print(c) # 加密 `123454321`,得到密文:`8922052926595796`
m = decrypt(c, N, d)
print(m) # 解密,得到明文 `123454321`RSA的安全性
RSA是一个简单的算法,(主流的)攻击思路也不复杂:解密是需要私钥 $(N, d)$ 的,那么目标就是取得 $d$;由于$d$是 $e$ 在模 $\varphi(N)$ 意义下的逆元,故只需要知道 $\varphi(N)$ 就可以由公钥推出私钥;而要想知道 $\varphi(N)$ 是多少,只需要质因数分解$N$——因此,一般认为,RSA的安全性取决于分解$N$的难度。
目前,分解质因数是极端困难的。人们没有找到多项式时间内分解质因数的做法。而生成一个质数却很简单——我们拥有判断一个数是否为质数的快速算法(例如Miller-Rabin算法),又有质数定理: $\Pi (n) \sim n/\ln n$ 保证了 $n$ 附近期望每 $\ln n$ 个数里面就有一个质数。想找到适合RSA的大质数 $p,q$,只需要随机生成很大的数,然后检验是不是质数,重复几次就可以达到目标。
尽管现在没有多项式时间内分解质因数的算法,但有些算法还是比较快的——例如 Pollard's rho. 此外,量子计算机上可以实现Shor算法,但目前没有多大的应用价值。推荐使用不低于2048位的密钥,这里的密钥长度是指模数 $N$ 的二进制长度。
生成RSA密钥对
ssh-keygen 程序可以造一个RSA密钥对,接下来这个密钥对可以用于git身份验证、ssh服务器身份验证等很多功能。
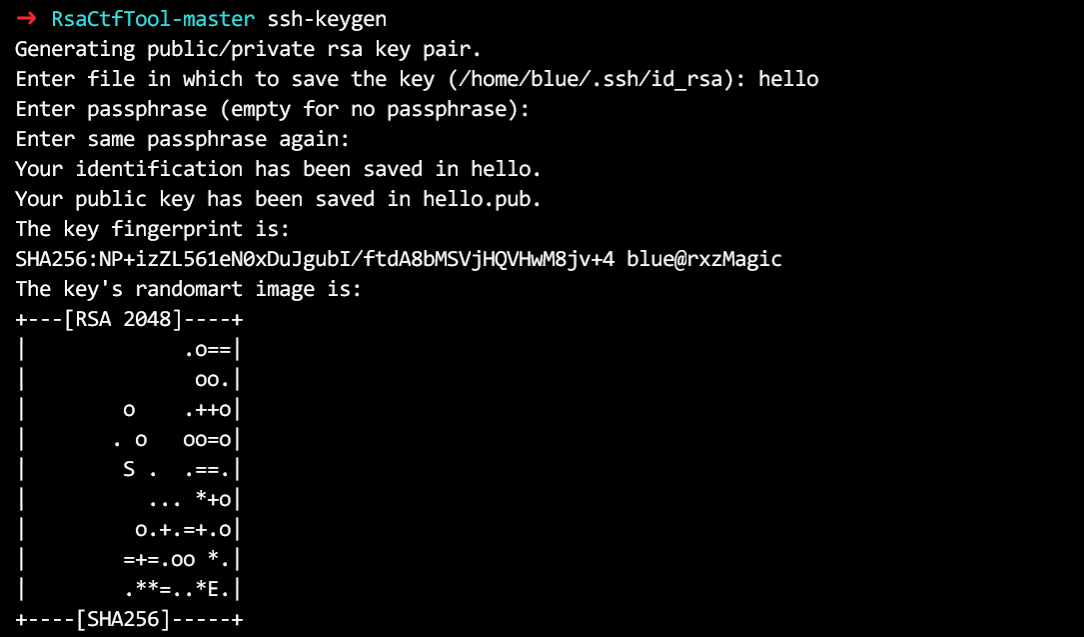
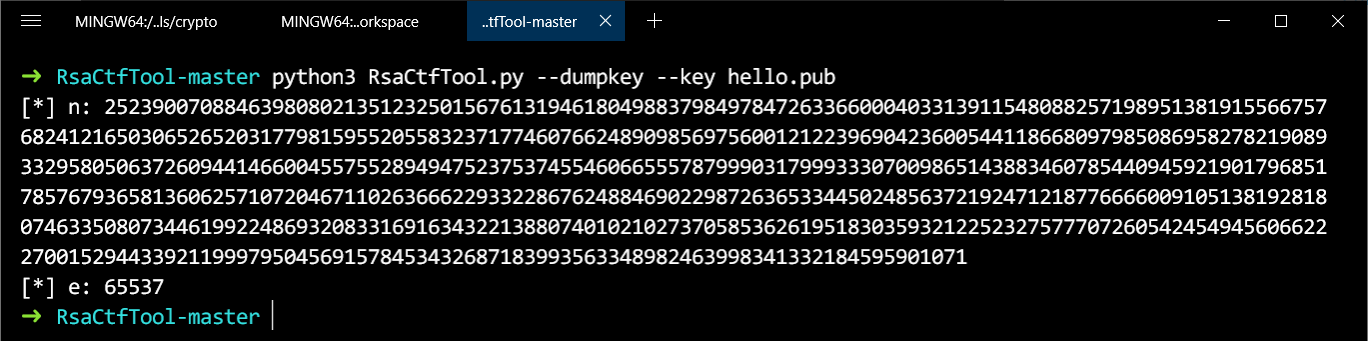
接下来,我们来看这里面有什么东西。 hello 是私钥文件, hello.pub 是公钥文件。里面的东西都是base64编码过的,可以用RsaCtfTool来查看。
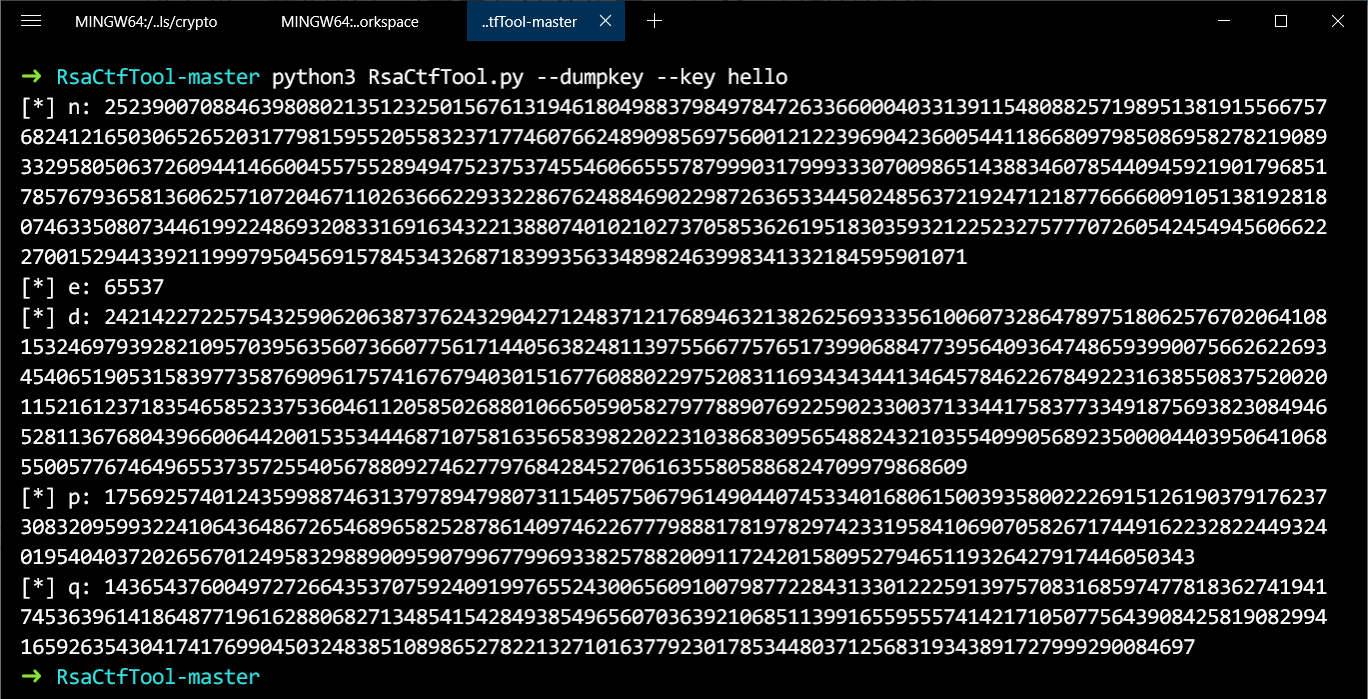
几道CTF题
Jarvis OJ: veryeasyRSA
已知RSA公钥生成参数:
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537, 求d
In [2]: p = 3487583947589437589237958723892346254777
In [3]: q = 8767867843568934765983476584376578389
In [4]: e = 65537
In [5]: phi = (p-1) * (q-1)
In [6]: gmpy2.invert(e, phi)
Out[6]: mpz(19178568796155560423675975774142829153827883709027717723363077606260717434369)JarvisOJ: Easy RSA
还记得veryeasy RSA吗?是不是不难?那继续来看看这题吧,这题也不难。
已知一段RSA加密的信息为:0xdc2eeeb2782c
已知加密所用的公钥:(N=322831561921859 e = 23)
请解密出明文,提交时请将数字转化为ascii码提交
In [2]: c = 0xdc2eeeb2782c
In [3]: n = 322831561921859
In [4]: e = 23
In [7]: !factor {n}
322831561921859: 13574881 23781539
In [8]: p = 13574881; q = 23781539
In [9]: phi = (p-1)*(q-1)
In [10]: d = gmpy2.invert(e, phi)
In [14]: hex(gmpy2.powmod(c, d, n))
Out[14]: '0x33613559'
In [16]: codecs.decode('33613559', 'hex')
Out[16]: b'3a5Y'BUUCTF: RSA
在一次RSA密钥对生成中,假设p=473398607161,q=4511491,e=17
求解出d作为flag提交
In [21]: p = 473398607161
In [22]: q = 473398607161
In [23]: e = 17
In [24]: gmpy2.invert(e, (p-1)*(q-1))
Out[24]: mpz(13182720074178117839153)BUUCTF: rsarsa
Math is cool! Use the RSA algorithm to decode the secret message, c, p, q, and e are parameters for the RSA algorithm.
(给定了 p, q, e, c)
Use RSA to find the secret message
In [25]: p = 96484230290105156765905517400104265349457376392357398006439893520398525072984913995610350091634 ...: 27050370107570733633350911691280297777160200625281665378483
In [26]: q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732 ...: 443992230647903887510065547947313543299303261986053486569407
In [27]: e = 65537
In [28]: c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605 ...: 6473166465764865262174570063768422808697285817267464015837058999417682141387422596893348407356335530 ...: 5388764184765117377625182029308721288567018036740680740676592363897316137581739273774783276275169010 ...: 4423869019034
In [29]: d = gmpy2.invert(e, (p-1)*(q-1))
In [30]: gmpy2.powmod(c, d, p*q)
Out[30]: mpz(5577446633554466577768879988)