椭圆曲线是什么

　　满足 Weierstrass 方程$$Y^ 2 = X ^ 3 + AX + B$$的点集，称为椭圆曲线(elliptic curve)。下面给出两个椭圆曲线的例子：

▲ 两个椭圆曲线。左图：$y^2 = x ^ 3 - 3x + 3$ ，右图： $y ^ 2 = x ^ 3 - 6x + 5$

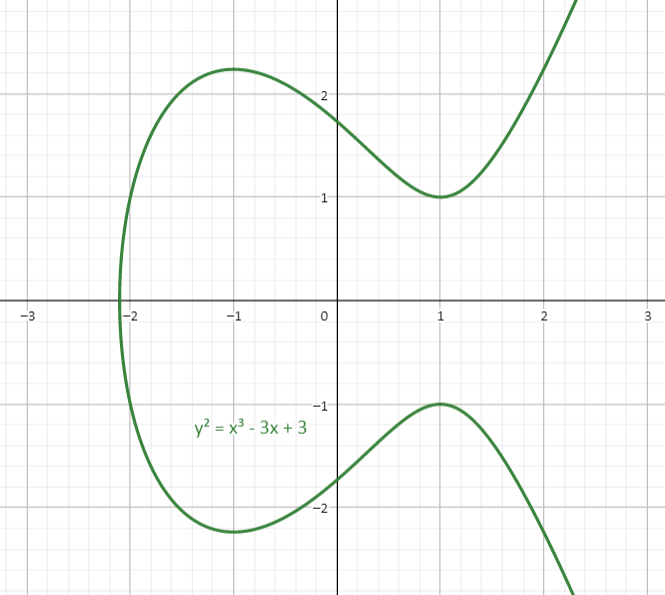
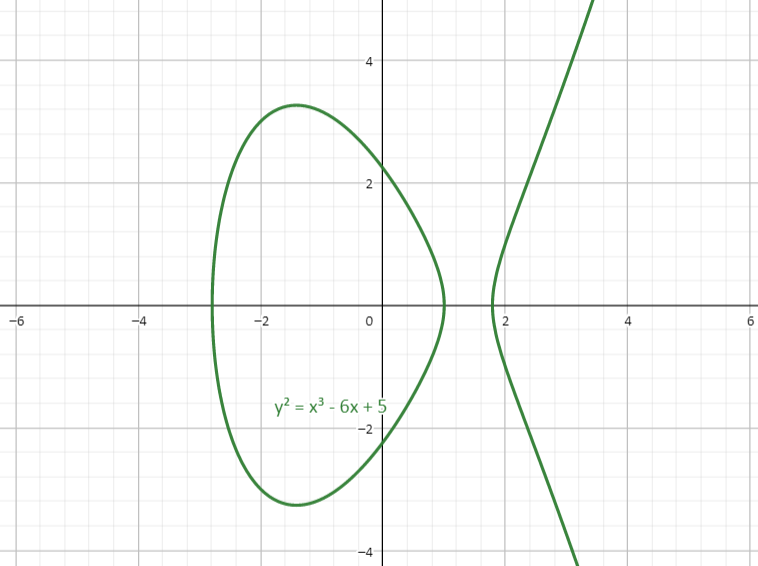
　　可见它的长相与椭圆并没有什么联系。我们可以在椭圆曲线 $E$ 上定义“加”的运算：假设有两个点 $P,Q$，则 $P$ 与 $Q$ 的和  $P\oplus Q$ 由如下步骤得到：

  • 连接 $PQ$ 形成一条直线，这条直线交 $E$ 于 $R$ 点。
  • $R$ 相对于 $x$ 轴的对称点，就是 $P\oplus Q$ 的结果 $R'$
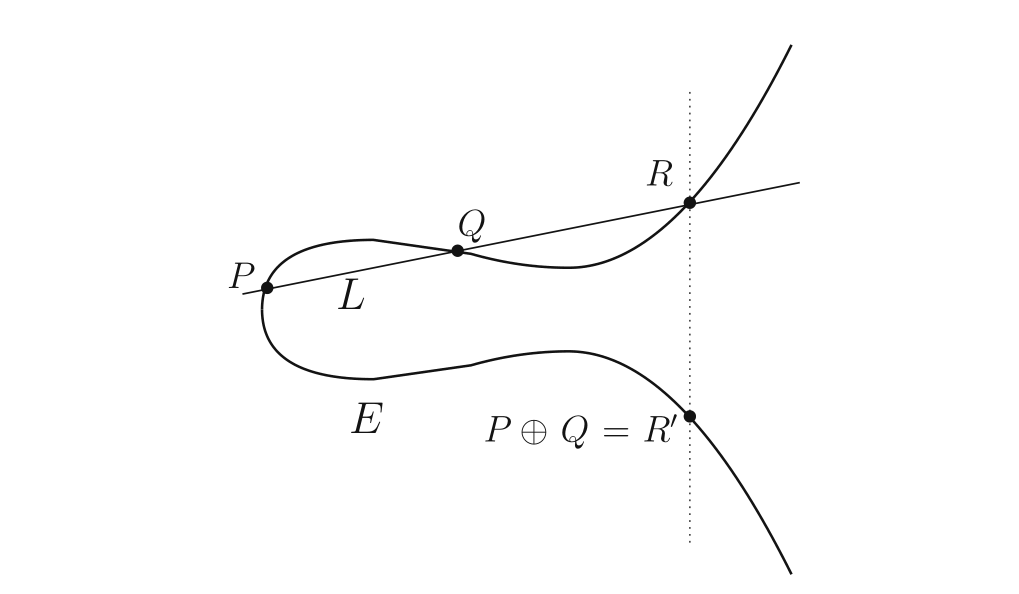
▲ 椭圆曲线上的加法。 图源：An Introduction to Mathematical Cryptography

　　这个运算的定义看起来很奇怪，不过我们马上就去证明它有非常优良的性质。

　　先展示一个例子：假设我们手上的椭圆曲线是 $E: Y ^ 2 = X ^ 3 - 15 X + 8$，P 点坐标是 $(7, 16)$，Q 点坐标是 $(1,2)$，如下图所示：

▲ 在 $E: Y ^ 2 = X ^ 3 - 15 X + 8$ 上计算 $(7,16) + (1,2)$

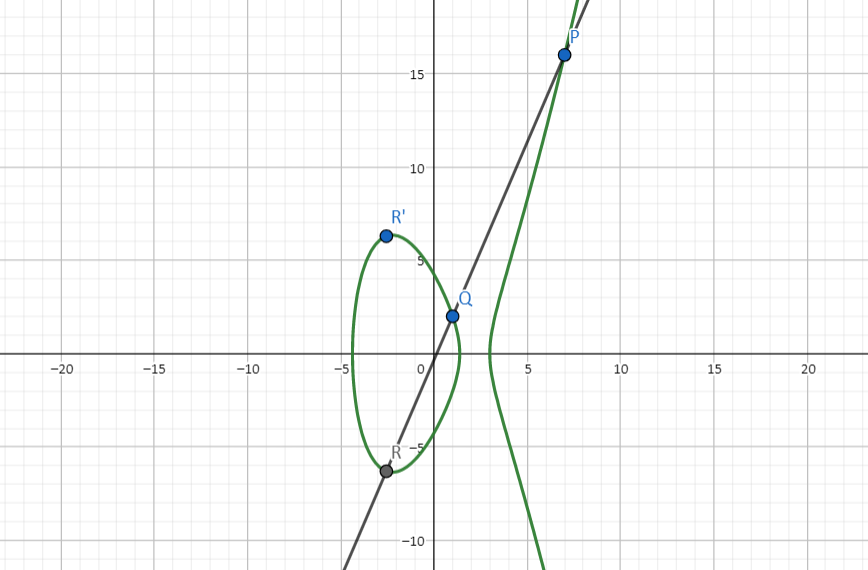
　　首先，需要获取 $PQ$ 这条直线的表达式。显然斜率为$$\lambda = \frac{x_P- x _Q}{y_P - y_Q} = \frac{7}{3}$$再代入点 $P$ 得到截距，于是得到了直线的表达式：$$PQ: Y = \frac{7}{3}X - \frac13$$用这里的 $Y$ 去替换方程 $E$ 左边的 $Y$，化简之后有：$$X^ 3 - \frac{49}{9}x^2 - \frac{121}{9} X + \frac{161}{9} = 0$$我们懒得直接解这个一元三次方程。注意到直线与 $E$ 交于三个点，那么上面这条方程等价于$$(x-e_1)(x-e _2)(x-e _3) = 0$$而我们已经知道了直线与 $E$ 的两个交点 $P,Q$，对应着 $x$ 的两个解 ，故有$$(x-7)(x-1)(x-e _ 3) = 0$$观察两个等价方程的零次项，有$$-7e_ 3 = \frac{161}{9} \quad \Rightarrow  \quad e _ 3 =  \frac{23}{9}$$x轴坐标知道了，y轴左边代进直线就知道。于是我们得到 $R=(-\frac{23}{9}, -\frac{170}{27})$，于是 $$P\oplus Q = R' = (-\frac{23}{9}, \frac{170}{27})$$

　　$P\oplus Q$的问题解决了，那么 $P\oplus P$ 呢？微积分的经验告诉我们，采用 $P$ 的切线来代替 $PQ$ 比较恰当。它仍然满足“直线与 $E$ 交于三个点”，只不过有两个点重合在 $P$. 反映到刚刚谈论的方程上，就是 $e_1 = e_2$. 此时 $e _3$ 仍然是很好求的。

▲ 在 $E$ 上进行 $P\oplus P$

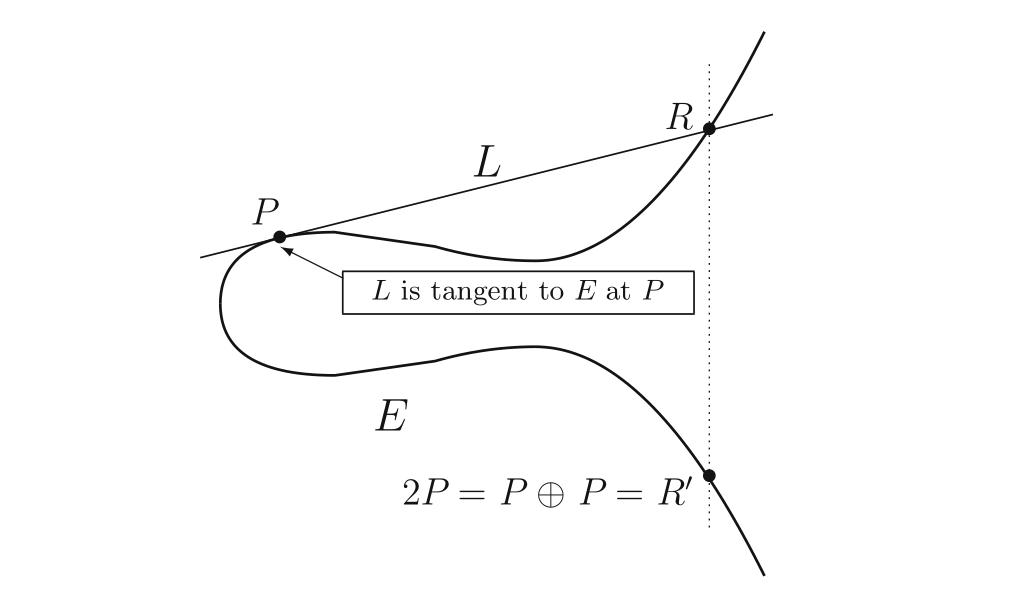
　　举个例子。还是用刚刚的椭圆曲线，$P = (7, 16)$。为了计算 $P \oplus P$，需要先求出 $P$ 点的切线方程。把方程 $E$ 左右都取微分，有$$2y dy = (3x ^ 2 - 15) dx$$从而在 $P$ 点，有$$\frac{dy}{dx} = \frac{3x ^ 2 - 15}{2y} = \frac{33}{8}$$于是得到直线方程：$$L: Y = \frac{33}{8}X - \frac{103}{8}$$回代到曲线 $E$：$$X^ 3 - \frac{1089}{64} X ^ 2 + \frac{2919}{32} X - \frac{9457}{64} = 0$$这个方程等价于交点方程：$$(x-7)(x-7)(x-e _ 3) = 0$$考察零次项，有$$-49e_3 = -\frac{9457}{64} \quad\Rightarrow\quad e_3 = \frac{193}{64}$$于是终于得到 $P\oplus P = (\frac{193}{64}, \frac{223}{512})$

　　计算确实挺麻烦的，但这里的运算全是四则运算，在计算机的帮助下可以飞快地完成。

无穷远点

　　我们解决了 $P\oplus Q$ 和 $P \oplus P$ 的问题，但这是不完备的——是不是任意两个点，都允许进行加法呢？我们刚刚的计算，取决于一个前提条件——连线也好，切线也好，与椭圆曲线都有三个交点，在已经知道其中两个交点的情况下，可以求第三个交点。但有的时候，$PQ$的连线与椭圆曲线只有两个交点！这种情况发生在 $P$ 和 $Q$ 关于 x 轴对称的情况下，如下图：

▲ 关于 x 轴对称的两个点，它们的连线与 $E$ 只交于两个点

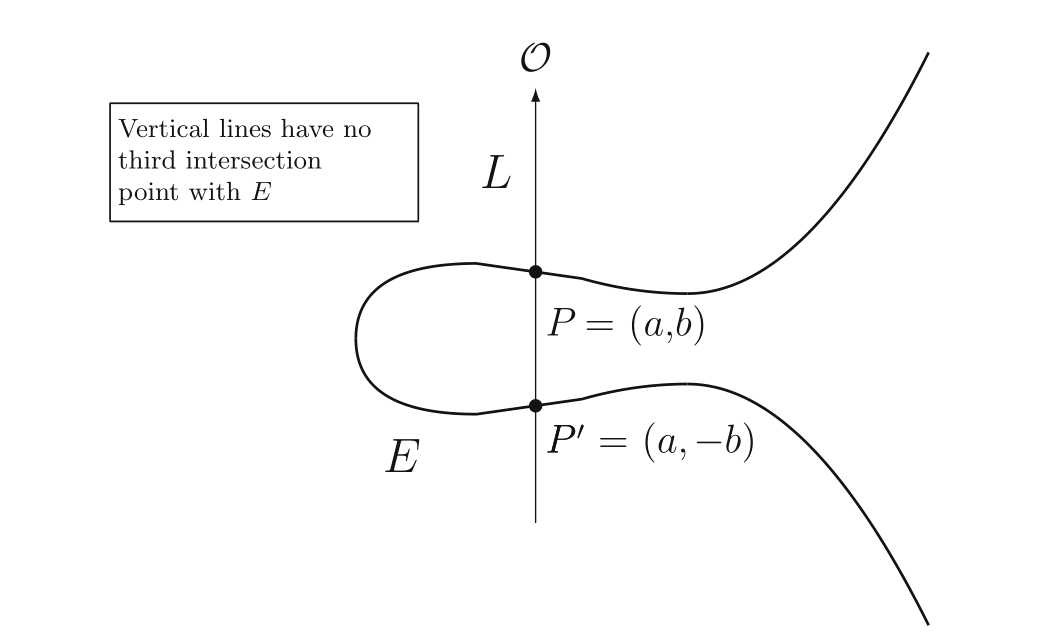
　　我们现在有两条道路：一种是声明这种情况下的加法不合法；第二种是引入一条特殊的加法规则，来解决困境。最终人们选择了第二种，那就是引入无穷远点。

　　假设 $P$ 与 $P'$ 的连线交 $E$ 于某个无穷远的点，记为 $\mathcal{O}$，也就是说：$$P \oplus P' = \mathcal{O}$$

　　需要注意的是，我们只引入了一个无穷远点，假想它在每一条铅直线上。

　　如果把某个点加上无穷远点，会发生什么情况呢？$P$ 与 $\mathcal{O}$ 的连线交 $E$ 于三个点—— $\mathcal{O}, P, P'$，于是把 $P'$ 作为直线与 $E$ 相交得到的点；再关于 x 轴对称一次，又回到了 $ P $. 这也就是说：$$P + \mathcal{O} = P$$

　　我们意识到，$\mathcal{O}$ 是加法运算的单位元。

椭圆曲线加法群

　　由于 $\mathcal{O}$ 的存在，任意两个点都是可加的。现在，带着刚刚引进的无穷远点 $\mathcal{O}$ ，我们重新定义椭圆曲线。

一个椭圆曲线(elliptic curve) $E$ 是满足 Weierstrass 方程 $$E: Y ^ 2 = x ^ 3 + AX + B$$ 的解集，以及无穷远点 $\mathcal{O}$. 其中 $A, B$ 满足$$4A ^ 3 + 27 B^2 \neq 0$$

　　先解释为什么要 $4A ^ 3 + 27 B^2 \neq 0$.

　　我们知道 $x^ 3 + Ax + B$ 可以表达为 $(x-p_1) (x - p_2) (x - p_3)$，此时当且仅当  $p_1, p_2, p_3$ 互不相同，才会有 $4A ^ 3 + 27 B^2 \neq 0$. 至于如果 $4A ^ 3 + 27 B^2 = 0$，会出现什么情况？

▲ 两条不合法的椭圆曲线

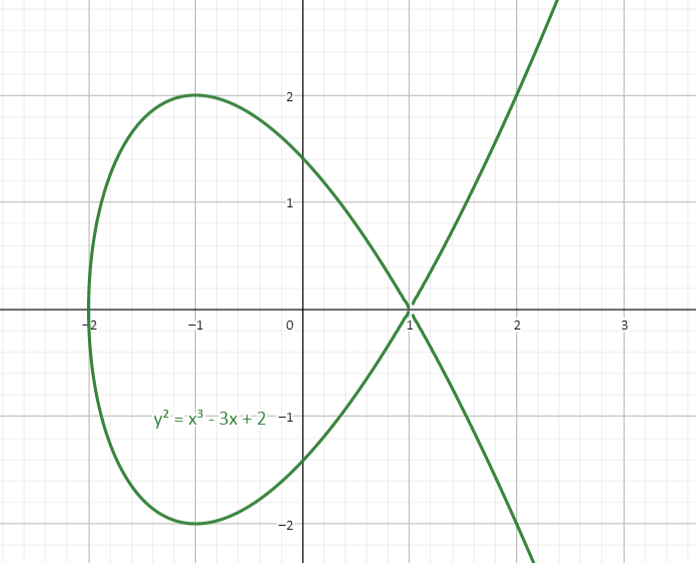
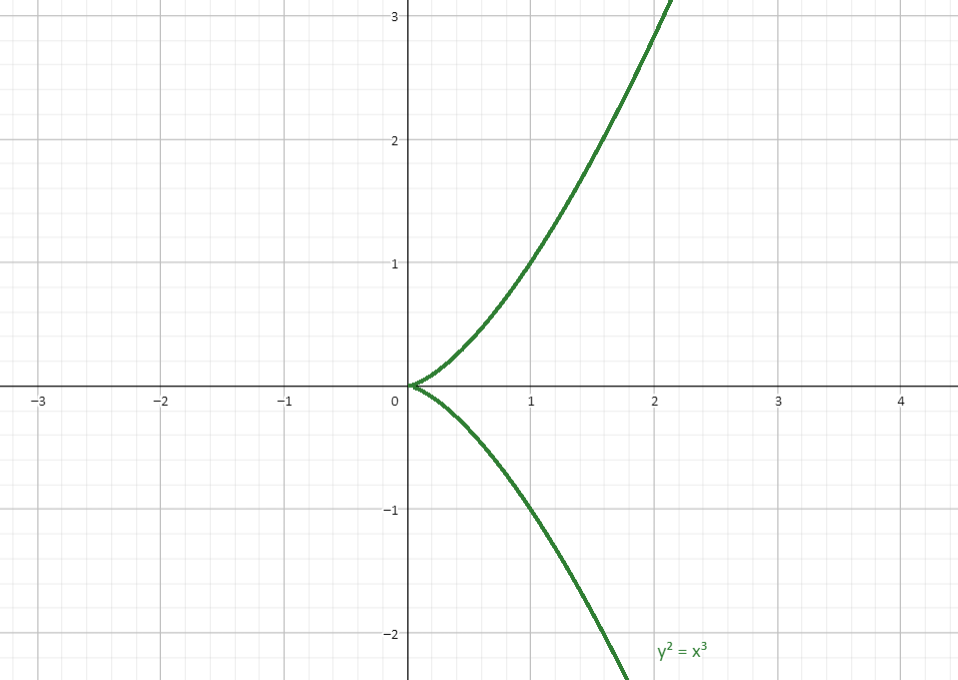
　　这与我们平常见到的两类椭圆曲线，长相差异有点大。它们存在奇点，这会导致我们一些算法失效（例如，左图中的 $(1,1)$ 加上自己应该等于什么呢？），既然如此，我们干脆不讨论这一类曲线，以后使用椭圆曲线的时候，都选用那些形态比较正常的。

　　在椭圆曲线上，$\oplus$ 满足加法的性质，以下简写为 “$+$”。我们有：

  • 有单位元：$P+O = O + P = P$.
  • 有逆元：$P+(-P) = \mathcal{O}$，其中 $-P$ 是 $P$ 关于 x 轴的对称点。
  • 结合律：$(P+Q)+R = P+ (Q+R)$
  • 交换律：$P+Q = Q+P$

　　以上每一条性质都可以手工验证。从而 $(E, +)$ 是一个阿贝尔群。于是立刻可以定义数乘运算：

对于正整数 $n$ 和椭圆曲线上的点 $P$，定义 $$nP = P+P+P+\cdots + P$$
显然，$nP$ 可以通过类似于快速幂的算法，以 $O(\log n)$ 次加法的代价求出来。
给定 $P$ 和 $Q=nP$，求解 $n$，就是椭圆曲线上的离散对数问题。

　　最后，我们给出离散对数加法算法的精确描述。设 $E: Y ^ 2 = X^3 + AX + B$ 是椭圆曲线，则可以使用如下算法计算 $P_1 + P_2$：

  1. 若 $P_1 = \mathcal{O}$，则 $P_1 + P_2 = P_2$.
  2. 否则，若 $P_2 = \mathcal{O}$，则 $P_1 + P_2 = P_1$.
  3. 否则，记 $P_1 = (x_1, y_1), P_2 = (x_2, y_2)$.
  4. 若 $x_1 = x_2$ 且 $y_1 = -y_2$，则 $P_1 + P_2 = \mathcal{O}$.
  5. 否则，记 $$\lambda = \begin{cases}\frac{y_2 - y_1}{x_2 - x_1},\quad  P_1 \neq P_2 \\ \frac{3x_1^2 + A }{2y_1}, \quad P_1 = P_2\end{cases}$$
    令$$x_3 = \lambda ^ 2 - x_1 - x_2, \quad y_3 = \lambda(x_1 - x_3) - y_1$$
    则 $P_1 + P_2 = (x_3, y_3)$.

　　上面的过程 (5) 和我们那套手工做法是一致的。

　　Sage为椭圆曲线提供了很好的支持。下面创建一个有理数域上的椭圆曲线：

E=EllipticCurve([-3,3])
show(E)
E.plot()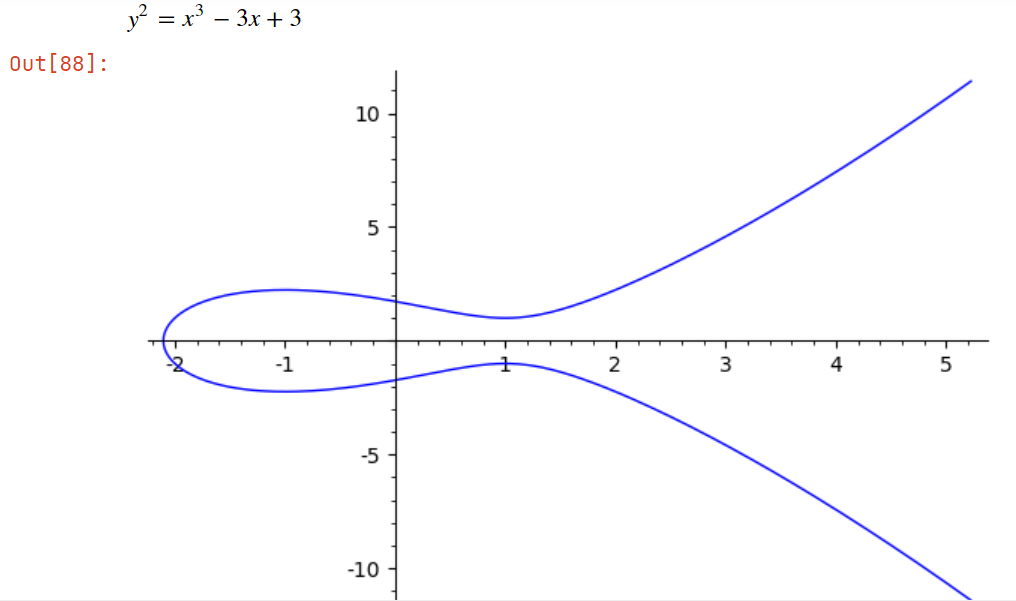
▲ Sage 创建椭圆曲线

　　可以获取 $x=1$ 时 $y$ 的坐标：

P = E.lift_x(1)
P.xy()
# (1, 1)

　　可以进行加法和数乘：

P = E(1, 1)
print((P+P).xy())
# (-2, -1)

print((10*P).xy())
# (-534970997642/1270419782641, -2930599739414754541/1431926979188367689)

　　单位元（无穷远点）用 E(0) 来得到。可以进行运算：

O = E(0)
P = E(1, 1)
print((O+O) == O)
# True

print((O+P).xy())
# (1, 1)

print((O+P) == P)
# True

　　现在我们造一个实数域上的椭圆曲线：

E=EllipticCurve(RealField(), [-15,8])
show(E)
E.plot()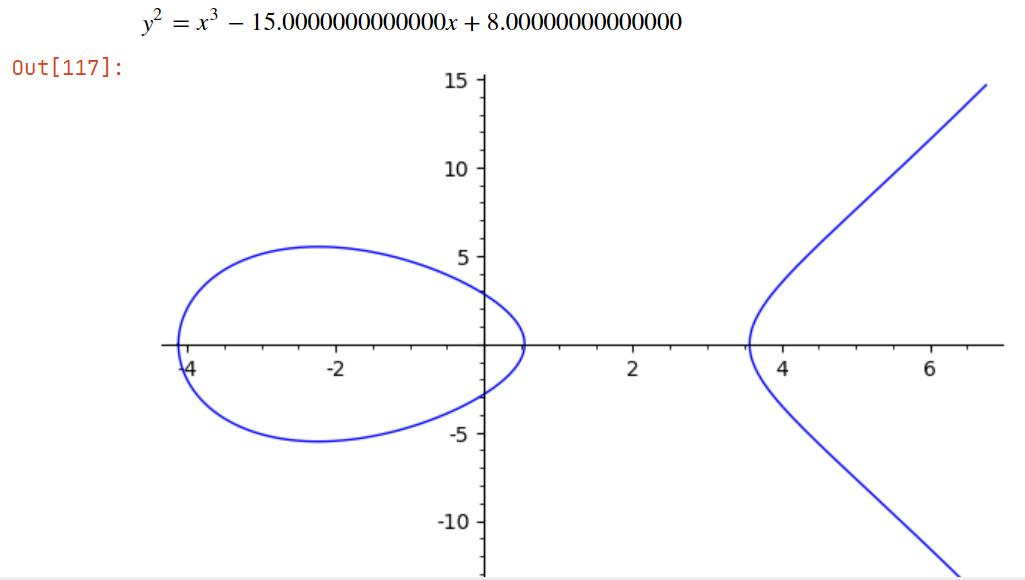
▲ 实数域上的椭圆曲线

　　运算：

P = E.lift_x(666)
Q = E.lift_x(233)

print(P.xy())
# (666.000000000000, 17187.1554947292)

print(Q.xy())
# (233.000000000000, 3556.10039228366)

print((P+Q).xy())
# (92.0216770365539, 881.967248744277)

print((100*(P+Q)).xy())
# (4.19546744213511, 4.34929697563973)

有限域上的椭圆曲线

　　密码学专注于离散的数学，而上面介绍的椭圆曲线是连续的。我们想把椭圆曲线及其加法应用于密码学，就需要在它上面定义一个有限群。

设 $p$ 为质数，有限域 $\mathbb{F}_p$ 上的椭圆曲线是下面的方程：$$E: Y^2 = X ^ 3 + AX + B\quad with ~ A,B \in \mathbb{F}_p, 4 A ^ 3 + 27 B ^ 2 \neq 0$$其点集为：$$E(\mathbb{F}_p) = \{(x, y) ~ : ~ x, y\in \mathbb{F} _ p , ~ y ^ 2 = x ^ 3 + Ax + B\} \cup \{ \mathcal{O} \}$$其中所有的运算在模 $p$ 意义下进行。

　　看一个例子。考虑 $\mathbb{F}_{13}$ 上的椭圆曲线$$E: Y^2 = X ^ 3 + 3 X + 8$$

　　想找出这个椭圆曲线上的点集，只需要枚举 $x$，然后看是不是有 $y$ 使得 $y ^ 2$ 等于 $x ^ 3 + 3x + 8$. 这是一个二次剩余问题，我们已经解决得比较好了。在 $x=0$ 的时候，没有 $y$ 与之对应；在 $x=1$ 的时候，$\sqrt{12} = 5, 8$，从而 $(1,5)$ 和 $(1, 8)$ 是椭圆曲线上的点。

　　Sage 可以在有限域上建立椭圆曲线，并枚举所有点：

E = EllipticCurve(GF(13), [3, 8])
E.points()
# [(0 : 1 : 0), (1 : 5 : 1), (1 : 8 : 1), (2 : 3 : 1), (2 : 10 : 1), (9 : 6 : 1), (9 : 7 : 1), (12 : 2 : 1), (12 : 11 : 1)]
▲ 枚举椭圆曲线上的所有点。 z 轴分量为 0 的是无穷远点，其余的是平凡点

　　在有限域椭圆曲线上进行加法：

E = EllipticCurve(GF(13), [3, 8])
print(E(1, 5) + E(1, 8))
# (0 : 1 : 0), 无穷远点

print(E(12, 2) + E(9, 7))
# (2 : 3 : 1)

　　来观察有限域 $\mathbb{F}_{13}$ 上的椭圆曲线的加法表：

▲ $F_{13}$ 上的椭圆曲线 $E: Y ^ 2 = X ^ 3 + 3 X + 8$ 的加法表

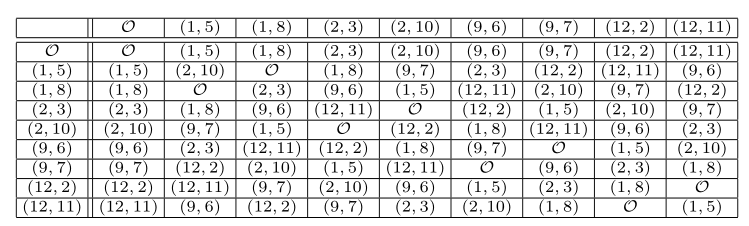
　　有限域上的椭圆曲线以及加法，构成了一个有限群。现在来研究这个群里的元素个数。我们知道，一个整数在有限域内，大概有一半的概率是二次剩余，一半的概率不是。所以我们猜测$$\text{card} ~ E(\mathbb{F}_p) \approx 50\% \cdot p \cdot 2 + 1 = p+1$$

　　这个猜测挺准确。事实上$$\text{card} ~ E(\mathbb{F}_p) = p+1 - t_p \quad where ~ |t_p| \leq 2\sqrt p $$

　　有限域上的椭圆曲线，点的分布与实数域上的椭圆曲线非常不同。来看两个例子。

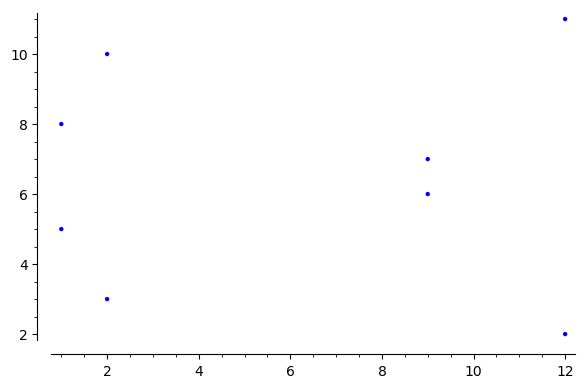
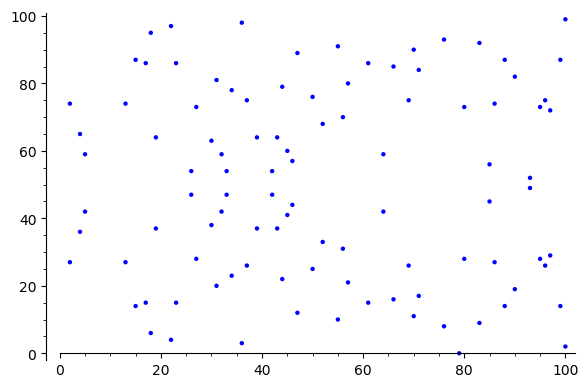
▲ 有限域上椭圆曲线的点分布。它们 $A=3, B=8$，左：$\mathbb{F}_{13}$，右：$\mathbb{F}_{101}$

　　在建立了“离散”的椭圆曲线之后，我们来看它的离散对数问题。

椭圆曲线离散对数问题

　　经典的椭圆曲线上的离散对数问题，是给定点 $P$ 和 $nP$，要推出 $n$ 的值。有限域椭圆曲线上的离散对数问题亦然。

设 $E$ 是有限域 $\mathbb{F}_p$ 上的椭圆曲线，$P, Q \in E(\mathbb{F}_p)$. 椭圆曲线离散对数问题(Elliptic Curve Discrete Logarithm Problem) 是指：找到一个整数 $n$ 使得 $Q = nP$. 我们记 $$n = \log_P(Q)$$并称 $n$ 是以 $P$ 为底 $Q$ 的椭圆曲线离散对数。

　　举一个离散对数的例子。考虑 $\mathbb{F}_{73}$ 上的椭圆曲线$$E: Y^2 = X ^ 3 + 8X + 7$$其上有点 $P=(32, 53)$ 和点 $Q=(39, 17)$. 计算得知 $Q=11P$，于是 $\log_P(Q) = 11$.

E = EllipticCurve(GF(73), [8, 7])
P = E(32, 53)
Q = E(39, 17)

P.discrete_log(Q)
# 11

　　很明显，符合条件的 $n$ 会有很多很多个，就像有限域上的离散对数也有无限多个一样。为了简化问题，我们定义 $P$ 的阶是使得 $xP = yP, x>y$ 的最小的 $s := x-y$，于是 $sP$ 显然就是无穷远点。顺带一提，由于拉格朗日定理，$s$ 是 $\text{card } ~ E(\mathbb{F}_p)$ 的因数。离散对数是一个解系，每个解可以表示成 $n_0 + k \cdot s, k\in Z$.

　　所以现在，离散对数的全体解，是集族 $\mathbb{Z}/s\mathbb{Z}$ 中的一个元素。以后可以直接取 $[0, p)$ 之间的一个代表元 $n_0$，来代表离散对数的解了。另外，我们发现$$\log_{P} (Q_1 + Q_2) = \log_{P} (Q_1) + \log_P (Q_2)$$

　　从而 $\log_P  :  E(\mathbb{F}_p) \to \mathbb{Z} / s\mathbb{Z}$ 是群 $E(\mathbb{F}_p)$ 到群 $\mathbb{Z} / s\mathbb{Z}$ 的一个同态映射！

　　最后，需要注意的一点是，并不是全体 $\log_P(Q)$ 都可以求出解。举个例子：在我们刚刚讨论的那条曲线上，存在 $(20, 65)$ 这个点，但它不是 $P$ 的倍数。群论上这是很好理解的，因为这一个 $P$ 的阶不等于 $E$ 的阶，它无法生成整个 $E$：

E = EllipticCurve(GF(73), [8, 7])

P.discrete_log(Q)
# ValueError: ECDLog problem has no solution

E.order(), P.order()
# (82, 41)
▲ 离散对数无解的情况

　　目前已知的最快的 ECDLP 算法，需要 $\sqrt{p}$ 次运算来求解 $E(\mathbb{F}_p)$ 上的离散对数问题。因此 ECDLP 是一个相当困难的问题。我们将在之后的几篇文章中，讨论基于椭圆曲线的密码学。

例题

Jarvis OJ: 简单ECC概念
已知椭圆曲线加密 Ep(a,b) 参数为 p = 15424654874903,
a = 16546484, b = 4548674875, G(6478678675,5636379357093)
私钥为 k = 546768，求公钥 K(x,y)
提示：K=kG

注：题目来源XUSTCTF2016

　　直接用 Sage 算出 $kG$ 就行。

E = EllipticCurve(GF(15424654874903), [16546484, 4548674875])
G = E(6478678675,5636379357093)

K = 546768 * G
K.xy()
# (13957031351290, 5520194834100)
# x+y = 19477226185390