1976年,Diffie-Hellman 密钥交换算法一声炮响,给我们带来了公钥密码学。以 DH 交换算法、RSA 密码体系等全新的密码体系为分水岭,密码学被划分成了泾渭分明的两部分——古典密码学和现代密码学。在数千年的历史上,古典密码学的发展可谓花样百出、脑洞大赛,其能提供的安全性,在现代计算机面前,已经不堪一击;而新生的现代密码学,为我们个人通信、商业机密的传送提供了强有力的保障。
1976年,Whitfield Diffie 和 Martin Hellman 发表的论文 New directions in cryptography 开篇就是:
WE STAND TODAT on the brink of a revolution in cryptography.
——IEEE Transactions on Information Theory Volume 22 issue 6 1976 [doi 10.1109_tit.1976.1055638] Diffie, W.; Hellman, M. -- New directions in cryptography
Diffie-Hellman 密钥交换算法,称为密码学史上的革命,是毫不为过的。它提出了一种方法,使得:即使双方所有的通讯都被监听,他们仍然可以约定好一个密钥,只有他们俩知道。
离散对数
离散对数是这样一个问题:在 $GF(p)$ 上,有一个原根 $g$. 今给定 $g, h\neq 0$,要求找出 $x$,使得$$g^x \equiv h \pmod p$$我们称 $x$ 为“以 $g$ 为底,$h$ 的离散对数”,记为 $\log_g(h)$. 之所以称其为对数,是因为它的表现和实数域上的对数非常像。离散对数也满足 $\log_g(ab) =\log_ga + \log_gb$. 事实上,离散对数 $\log_g$ 是一个 $F ^ *_p$ 到 $Z/(p-1)Z$的群同构。
离散对数的计算是很困难的,因为离散对数的分布没有什么规律性可言。下面给出 $627^i \bmod 941$ 的分布情况:
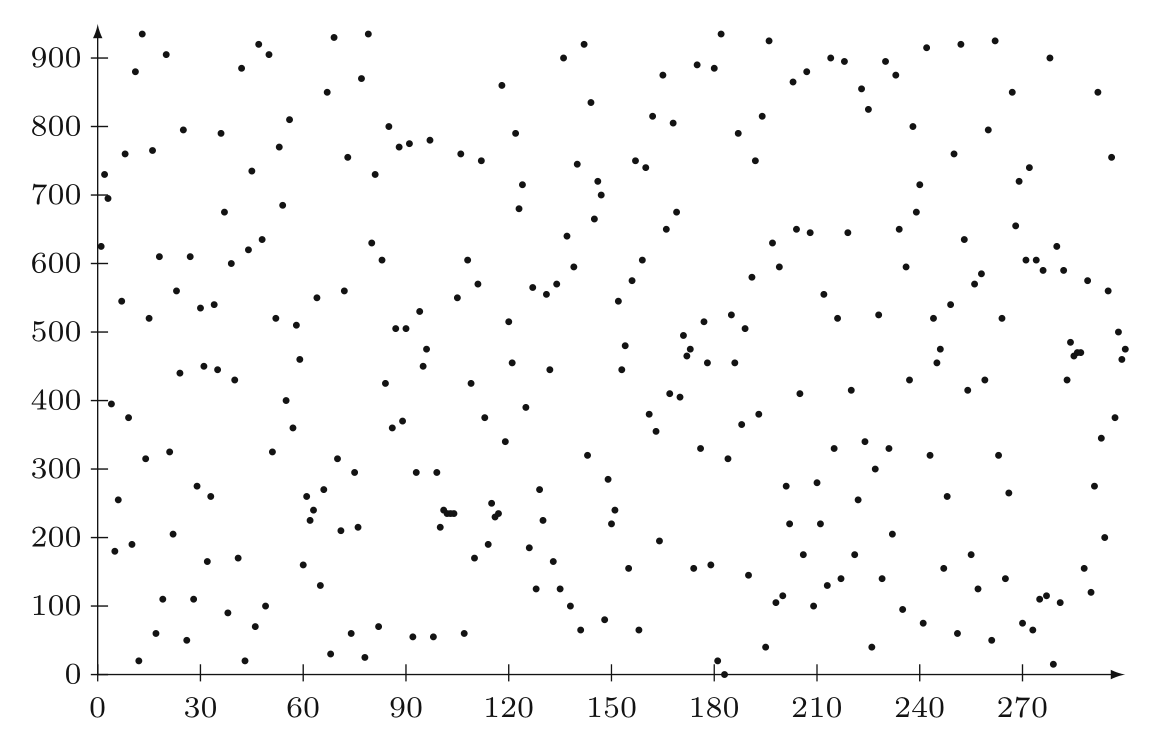
离散对数的计算是数学上一个公认的困难问题——目前来讲,我们没有找到多项式算法来求离散对数。在下一篇博客,我会介绍大步小步算法、Pohlig–Hellman 算法,它们能够较快地求离散对数,但仍然不是多项式的。大步小步算法可以在 $O(\sqrt{\text{ord} (g)})$ 的时间复杂度内求出某个数的离散对数,其中 $\text{ord}(g)$ 是 $g$ 在群 $GF(p)$ 中的阶。
Diffie-Hellman 密钥交换算法
现在假设 Alice 想和 Bob 约定一个整数作为密钥,但 Alice 与 Bob 素昧平生,且他们通信的信道是完全被监听的。在此情况下,我们的目标是,设计一个方案:经过几次通讯,Alice 和 Bob 掌握了一个相同的整数(密钥),而窃听者 Eve 无法知道这个密钥。
DH 密钥交换算法的思路是:既然求解离散对数是困难的,那么我们可以把信息隐藏在 $g$ 的指数中。传递 $g^x$ 可以使得窃听者无法获取$x$. 于是有了以下算法(下面所有运算在 $F_p$ 进行):
- Alice 和 Bob 随便通过什么渠道,达成共识 $(g, p)$. 其中 $p$ 是一个质数,$g$ 是它的一个原根。
- Alice 想一个随机的数 $x$,算出 $A = g^x$,把 $A$ 发送给 Bob.
Bob 想一个随机数 $y$, 算出 $B=g^b$,把 $B$ 发送给Alice. - Alice 接到 $B$ 之后,计算 $B^a$ 作为协商好的密钥。
Bob 接到 $A$ 之后,计算 $A^ b$作为密钥。
为什么 Alice 和 Bob 计算出来的密钥是一样的?因为$$B^a = (g ^ b) ^ a = (g ^ a)^ b = A ^ b$$
为什么尽管 Eve 监听了所有的对话,仍然没法知道密钥?因为 Eve 只知道 $g, p, A, B$. 仅凭这些信息,想得到 $B ^ a$ 是很困难的。因为 $a$ 只能通过求离散对数获得;而我们刚刚讲过,求离散对数非常困难,只要他俩选个 1000-bits 的 $p$,且原根 $g$ 不乱选,则 Eve 很难得到 $a,b$ 中的任意一个,自然也就没法计算出 $g ^ {ab}$ 了。
下面举一个例子来演示 DH 密钥交换算法。Alice 和 Bob 选择了 $p=941, g=627$. 现在 Alice 心里想了一个数 $a=347$, 算出 $A = g ^ a = 390$. Bob 选的数是 $b=781$, 算出 $B = g ^ b = 691$. 现在他们公布 $A, B$. Alice 计算出 $B ^ a = 470$,Bob 计算出 $A ^ b = 470$, 于是 470 就是他们约定好的密钥。
Eve知道$p=941, g=627, A=390, B=691$,但她没法计算出密钥。至此,我们在不安全的信道里,完成了一次安全的密钥交换。可谓出淤泥而不染。
Elgamal 公钥加密算法
尽管 Diffie-Hellman 很好地完成了交换密钥的任务,但密钥毕竟不带有信息,无法直接用于通讯。Elgamal 公钥加密算法解决了通讯的问题。描述如下(下面所有运算在群$GF(p)$中进行):
- Alice 选取一对 $(g, p)$, 自己想一个 $a$ 作为私钥,然后计算出 $A= g ^ a$ 作为公钥。
Alice 将 $(g, p, A)$ 公布给所有人。 - Bob 现在想给 Alice 传送一条信息 $m$. 于是 Bob 选取一个随机数 $k$, 计算出 $$c_1 = g^k , \qquad c_2 = m A ^ k$$然后将$(c_1, c_2)$ 发送给 Alice.
- Alice 拿到 $(c_1, c_2)$,计算$$c_1^{-a}\cdot c_2 = g ^ {-ka} \cdot m \cdot g^{ak} = m$$于是 Alice 成功获取到了信息 $m$.
Elgamal 的安全性与 DH 是一致的。证明过程很巧妙:
- 如果攻击者可以攻破 Elgamal,那么攻击者也能攻破 DH.
设攻击者手上有一台魔法机器,给定 $p, g, A$,输入 $(c_1, c_2)$ 就可以输出 $m = c_1^{-a}\cdot c_2$. 那我们给这台机器输入 $(B, 1)$, 则机器会输出 $B ^ {-a}\cdot 1 = g ^ {-ab} $. 我们拿到这个结果,求一下逆元,就得到了 $ g ^ {ab}$. 从而拿到了 DH 的密钥。 - 如果攻击者可以攻破 DH,那他也能攻破 Elgamal.
设攻击者手上有一台用于攻击DH的机器,输入 $(g ^ a, g ^ b)$,会输出 $g ^ {ab}$. 那我们给它输入 $(c_1, A) = (g^k, g ^ a)$,机器会输出 $ g ^ {ka}$. 于是我们可以拿到 $g ^ {-ka}$. 现在计算 $$g ^ {-ka} \cdot c_2 = g ^ {-ka} \cdot m \cdot g ^ {ak} = m$$ 于是拿到了信息,攻破 Elgamal.
上述过程证明了 DH 与 Elgamal 的攻击难度是一样的。如果 DH 是安全的,则 Elgamal 也是安全的。但是 DH 的安全性不等于离散对数的安全性——如果离散对数可以快速求出来,则 DH、Elgamal 被攻破;但如果 DH 被攻破,走的可能不是离散对数的路子。我们只能说:离散对数是一个比 DH 更难的问题。
目前为止,Diffie-Hellman 密钥交换算法是安全的。它被用于 SSL 协议的握手阶段。
