题目来源:
不保证正确性!
T1
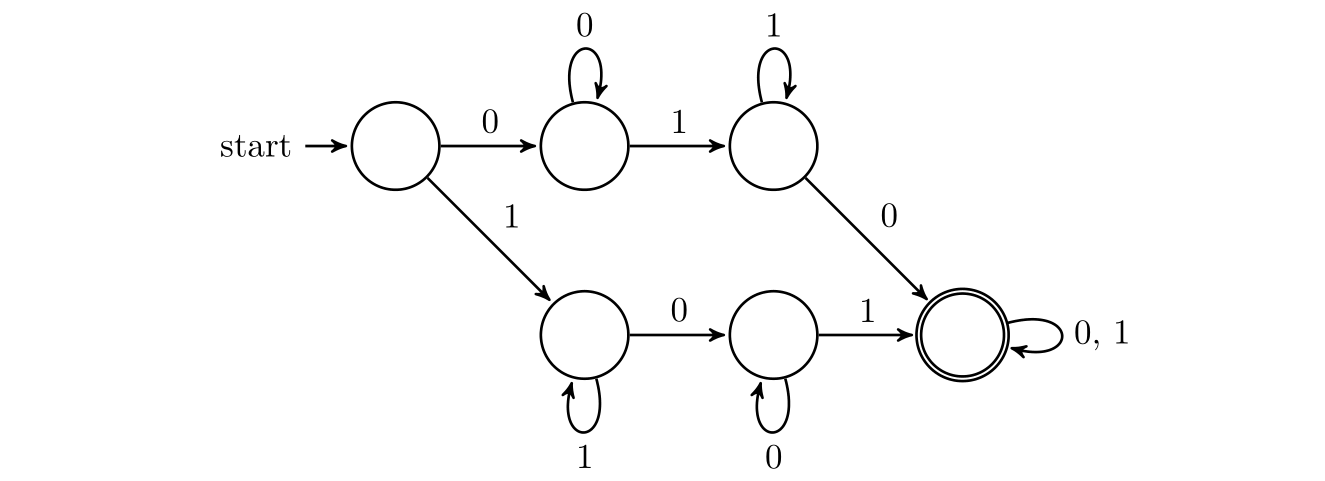
Design a DFA for the language $$L=\{w\in\{0,1\}^* \mid w \text{ contains both 01 and 10 as substrings} \} $$
解:如果字符串以 0 开头,那么它属于 $L$ 当且仅当出现一个 1、在 1 后面存在 0,也就是说,这个字符串形如 $0^+ 1 ^ + 0 (0+1) ^ *$. 若字符串以 1 开头,那么它属于 $L$ 当且仅当出现一个 0、在 0 后面存在 1,即 $1 ^ + 0 ^ + 1 (0+1) ^ *$. 设计 DFA 只需要分类讨论这两种情况,如下:
T2
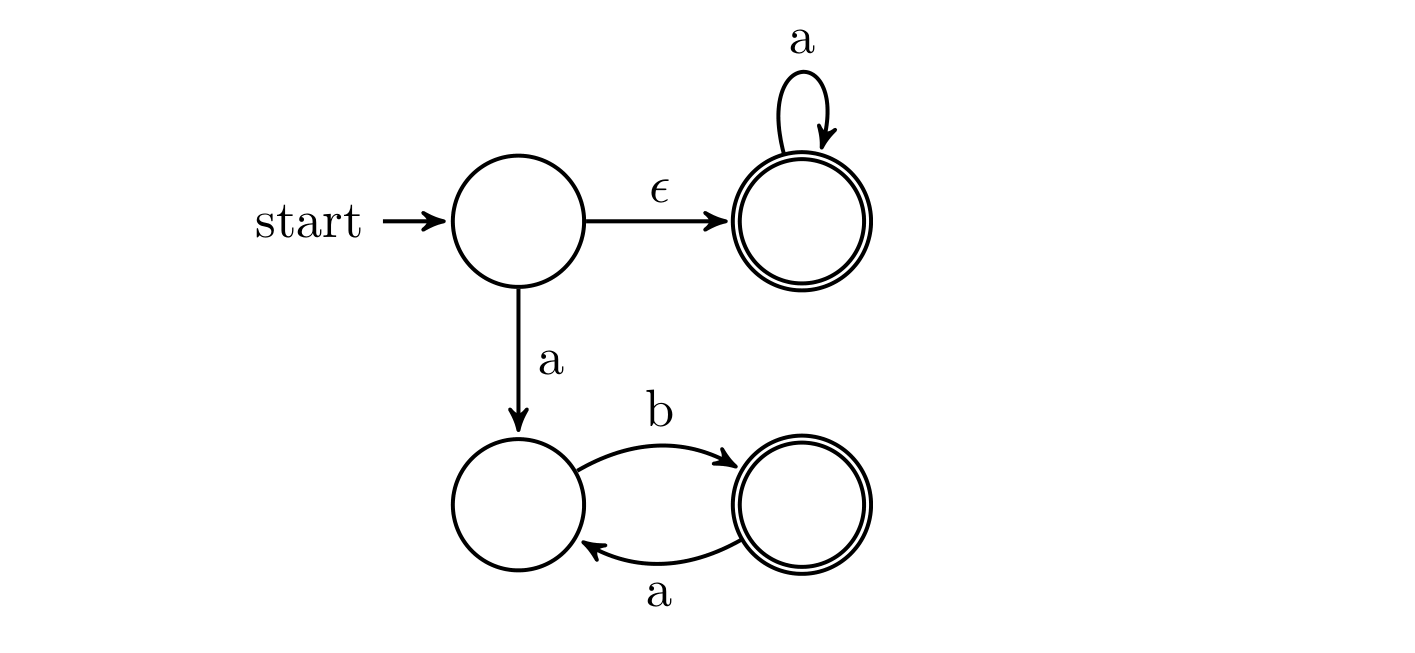
Design a NFA within four states for the language $\{a\} ^ * \cup \{ ab \} ^ *$.
解:题目要求采用不超过 4 个状态设计 NFA 识别这个语言。也是分类讨论即可,需要注意不能从 $ab$ 的接受点往起点连线,否则会让 $ababaaaaa$ 这种串被接受。
T3
Design regular expressions for language over $\Sigma = \{0, 1\}$
- All strings contain the substring 001.
- All strings expect the string 001.
解:
- $(0+1) ^ * (001) (0+1) ^ *$
- 需要排除掉上述这种情况。我们枚举长度为1、2、3的串来排除掉 001,接受长度大于 3 的所有串。结果如下:$$\begin{aligned}\epsilon & + (0+1) + (0+1)(0+1) \\ & + (0+1)(0+1)0 + 011+101+111 \\ & +(0+1)(0+1)(0+1)(0+1)(0+1) ^ *\end{aligned}$$
T4
Prove that $L = \{0 ^ m 1 ^ n \mid m/n\text{ is an integer}\}$ is not regular with pumping lemma.
证:假设 $L$ 是正则语言。那么我们取 $w = 0 ^ {2N} 1 ^ {2N} \in L$.
$w$ 可以被划分为 $xyz$ 且 $|y|>0, ~|xy| \leq N$.
那么一定有 $x=0 ^ a, ~ y=0^b$,其中 $a+b \leq N, b>0$.
于是 $x y ^0 z = 0 ^a 0 ^ {2N - a - b} 1 ^ {2N} \in L$,然而显然 $0< (2N-b)/(2N) < 1$ 不是整数,推翻假设。
T5
Convert the following NFA into DFA with subset construction.

解:子集构造法即可。$$\begin{array}{r|ll}
& 0 & 1 \\
\hline
\to p & \{p\} & \{p, q,r\} \\
q & \{r\} & \{r\} \\
r & \{s\} & \{s\} \\
s & \varnothing & \varnothing \\
\hline
\to\{p\} & \{p\} & \{p,q,r\} \\
\{p,q,r\} & \{p,r,s\} & \{p,q,r,s\} \\
*\{p,r,s\} & \{p,s\} & \{p,q,r,s\} \\
*\{p,s\} & \{p\} & \{p,q,r\} \\
*\{p,q,r,s\} & \{p,r,s\} & \{p,q,r,s\} \\
\end{array}$$
T6
Give a context-free grammar for $L=\{a ^ i b ^ j c ^ {i+j}\mid i,j \geq 0\}$.
解:注意到接受的字符串可以写成 $a^i (b ^ j c ^ j) c ^ i$ 的形式。构造出括号里面那个东西,再套壳即可。$$\begin{aligned}S &\to aSc \mid E \\
E &\to bEc \mid \varepsilon \end{aligned}$$
T7
Let L be the language generated by the grammar $G$ below
$$\begin{aligned}S & \to AB\mid BBB \\
A&\to Bb\mid \varepsilon \\
B&\to aB\mid A\end{aligned}$$
- 消除空产生式
- 消除单元产生式
- 转换到CNF
解:
- 注意到 $A,B,S$ 均可空。于是构造 $G ^ \prime$:$$\begin{aligned}S & \to A \mid AB \mid B \mid BB \mid BBB \\
A&\to b \mid Bb\\
B&\to a \mid aB\mid A\end{aligned}$$ - 上面的单元对有 $[B,A],[S,A],[S,B]$. 先抹掉所有单元产生式:$$\begin{aligned}S & \to AB \mid BB \mid BBB \\
A&\to b \mid Bb\\
B&\to a \mid aB\end{aligned}$$ 再复制子产生式到父亲,得到结果 $$\begin{aligned}S & \to AB \mid BB \mid BBB \mid b \mid Bb \mid a \mid aB \\
A&\to b \mid Bb\\
B&\to a \mid aB \mid b \mid Bb\end{aligned}$$ - 要命。。。$$\begin{aligned}S&\to AB \mid BB \mid BD _ 1 \mid b \mid B C_b \mid a \mid C_a B \\
D _ 1 &\to BB \\ C_a &\to a \\ C_b &\to b \\ A &\to b \mid BC_b \\ B &\to a \mid C_a B \mid b \mid BC_b\end{aligned}$$
T8
Design a PDA for $L=\{w\in \{a,b\} ^ * \mid w\text{ has more a's than b's}\}$.
解:往栈里面填字符。如果栈顶字符与自己互异,则弹掉栈顶;否则把自己压入栈顶。不难注意到栈里面的元素一定是同一种。当且仅当栈顶为 a 的时候,字符串可接受。
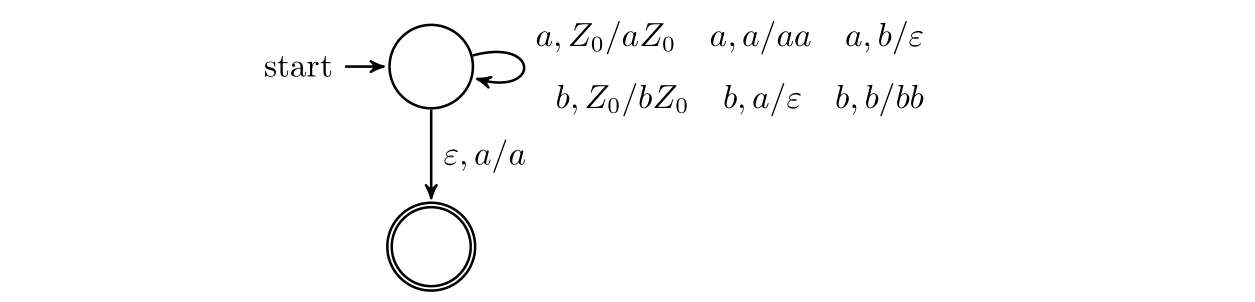
T9
Prove : for every context free language $L$, the language $$L^ \prime = \{ 0 ^ {|w|} \mid w \in L \}$$ is also context free.
证:考虑同态映射 $h(a)=0$. 则 $h(w) = 0 ^ {|w|}$.
注意到 $L$ 是上下文无关的,故 $h(L) = \{ 0 ^ {|w|} \mid w \in L \} = L ^ \prime$ 也是上下文无关的。
T10
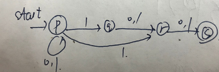
Design a Turing Machine that computes the following function $f: 0 ^ n\mapsto \text{binary}(n)$
Where integer $n\geq 1$ and $\text{binary}(n)$ is the binary representation of n.
For example: $f(0^3) = 11, f(0 ^5) = 101$.
解:有点难的题。基本思路是维护一个二进制累加器,去数 $0$ 的个数。每次数 0,都删去最右边那个 0 ,然后跑去把二进制累加器增加一次。我把累加器放在了输入进来的纸带的左边,因为二进制累加器是向左扩展的。累加器与输入串之间用一个 B 做间隔。
最后设计出来的图灵机如下。懒得用 Latex 画了,偷懒手绘一下:
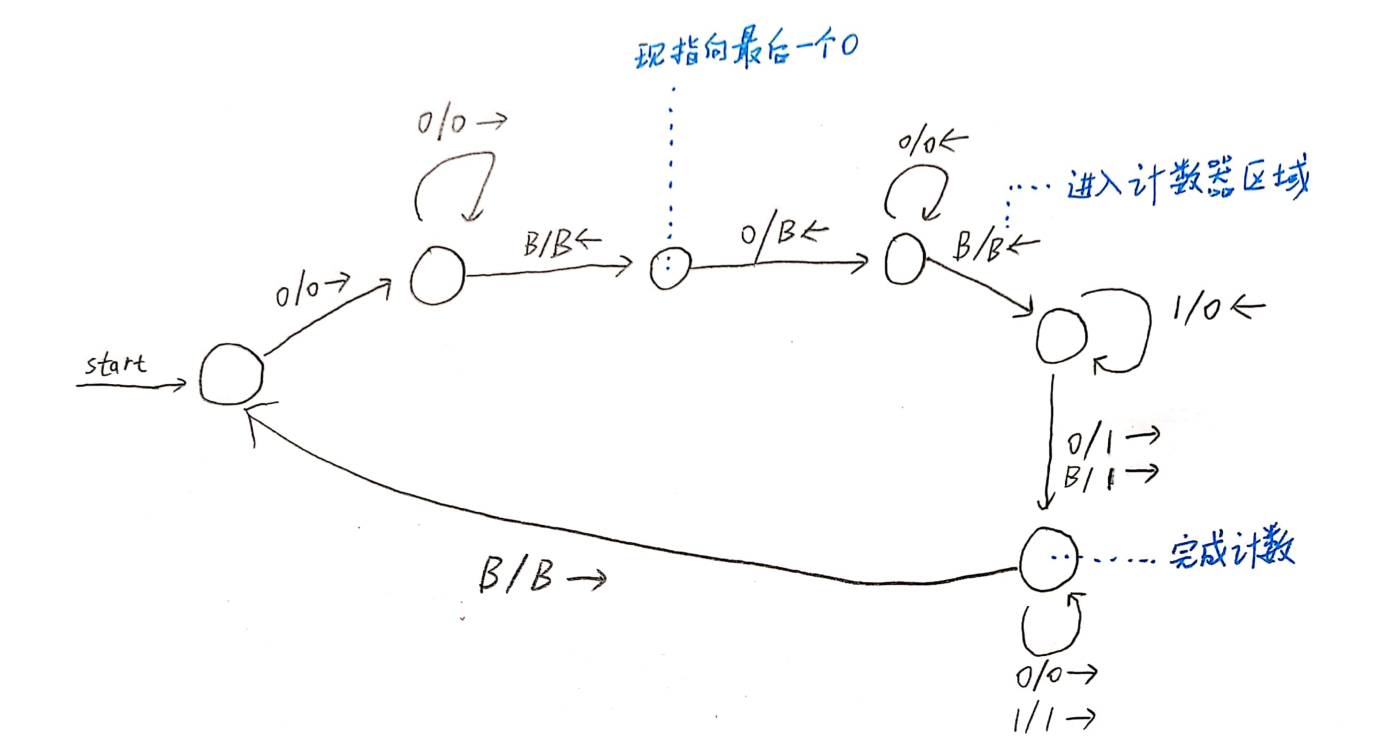
在图灵机停机之后,纸带上剩下的就是想要的二进制串。
